400-8899-570

      

      数字差分算法和涡街流量计的精度是两个相对独立的概念，但它们在某些情况下可能会相互关联，尤其是在涡街流量计的数据处理中。

      首先，数字差分算法是一种用于快速计算数列前缀和变化的技术，它通过计算原始数列中相邻元素之间的差值来形成差分数组，进而可以高效地处理数列的加减操作‌。
      这种算法在数据处理和信号处理中非常有用，但它本身并不直接决定涡街流量计的精度。‌
      差分算法的核心思想，是通过预处理出数组的差分数组，‌使得在修改区间时，‌只需修改两个位置的值，‌即可完成区间修改。
      ‌然后，‌再通过差分数组求出原数组。‌差分数组表示原数组中相邻两个元素之间的差值。‌对于区间加的操作，‌只需在差分数组的对应区间起点位置加上增量，‌终点位置的下一个位置减去增量。‌

      差分算法主要用于解决对不确定区间进行多次加减操作的问题，‌可以将时间复杂度从O(nm)降低到O(n)，‌但需要注意，‌差分算法只适用于加减操作，‌不适用于乘除操作。‌

      

      ‌涡街流量计是一种用于测量流体流量的仪表，其精度受到多种因素的影响，包括但不限于流量计的设计、制造质量、安装条件、流体特性以及数据处理方法等‌。
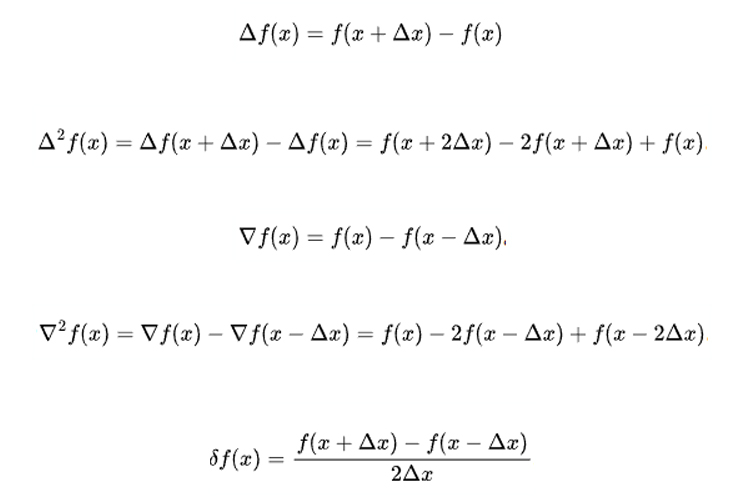
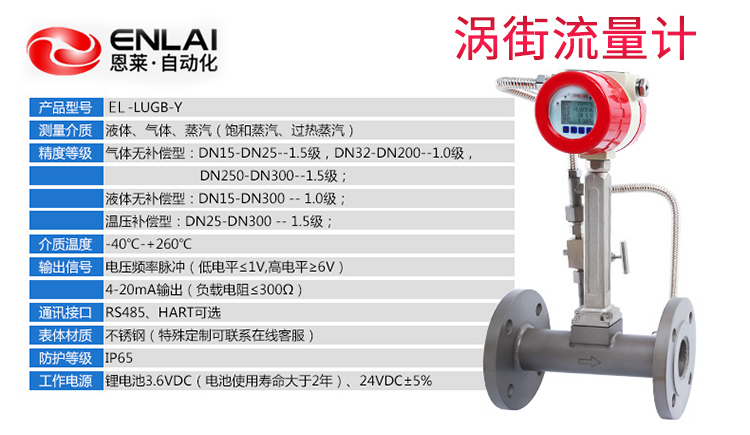
      涡街流量计通常具有高精度，其测量精度可以达到±(1～1.5)%R或更高，具体取决于流量计的类型、规格和使用条件‌。
      在涡街流量计的数据处理中，可能会使用到数字滤波、互相关算法、小波变换滤波算法等技术来提高信号的信噪比和测量精度。
      这些算法可以对涡街流量计输出的信号进行预处理或后处理，以减少噪声干扰和误差，从而提高测量精度‌。
      然而，这些算法的选择和应用需要根据具体的测量需求和条件来确定，并且需要仔细评估其对测量精度的影响。
      综上所述，数字差分算法本身并不直接决定涡街流量计的精度，但涡街流量计的数据处理中，可能会使用到类似的算法来提高测量精度。

      因此，在选择和使用涡街流量计时，需要综合考虑多种因素，包括流量计本身的精度、数据处理方法以及使用条件等。